3. Class method reference¶

Below is a detailed description of all available Classes and functions.

3.1. Points¶

class sgl.point.Point(x1, x2, x3)¶

class sgl.point.Point(iterable)

class sgl.point.Point(Vector)

A Point represents a single Point in 3D space. You can create a point by giving either three coordinates as parameters, or a list with three elements, each being a coordinate, or by giving a Vector.

classmethod origin()¶
classmethod o()¶: Returns the origin, that is the Point with coordinates (0, 0, 0)

__getitem__(n)¶

Returns the nth coordinate of the point:

Point(x1, x2, x3)
n:    0   1   2

>>> p = Point(13, 3, 7)
>>> p[0]
13
>>> p[1]
3
>>> p[2]
7

pv()¶

Returns the position vector of the point, this is a Vector that has the same coordinates as the point:

>>> p = Point(13, 3, 7)
>>> p.pv()
Vector(13, 3, 7)

moved(vector)¶

Returns the point that you get when you move self by vector:

>>> p = Point(13, 3, 7)
>>> v = Vector(29, 1, -5)
>>> p.moved(v)
Point(42, 4, 2)
>>> # Equivalent to
... Point(p.pv() + v)
Point(42, 4, 2)

3.2. Vectors¶

class sgl.vector.Vector(x1, x2, x3)¶

class sgl.vector.Vector(iterable)

class sgl.vector.Vector(Point, Point)

The Vector class represents a vector in 3D space. You can construct a vector either by giving the three coordinates directly (1st form), by giving an iterable that yields the three coordinates (like a list) (2nd form) or by giving two Points. The vector will then go from the first point to the second (3rd form).

Vectors support the following calculations: (a and b are vectors, c is a real number)

Operation	Result
a + b	Sum vector
a - b	Difference vector
c * a	Multiple of a vector
a * b	Dot product/inner product/ scalar product
abs(a)	Magnitude/length of a vector
-a	Reverse vector (same magnitude, reversed direction)
a[n]	nth coordiante of the vector

classmethod zero()¶: Returns Vector(0, 0, 0)

angle(other)¶

Return the angle (in radians) between two vectors:

>>> a = Vector(3, 0, 0)
>>> b = Vector(42, 0, 0)
>>> a.angle(b)
0.0

cross(other)¶: Return the cross product between two vectors, as defined by

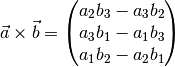
$\vec{a} \times \vec{b} = \begin{pmatrix}a_{2}b_{3} - a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2} - a_{2}b_{1}\end{pmatrix}$

length()¶: Returns the length (or magnitude) of the vector, a.length() = abs(a)

normalized()¶

unit()¶

Returns the normalized version of the vector, that is a vector that has the same direction but length 1:

>>> v = Vector(0, 3, 0)
>>> v = v.normalized()
>>> v
Vector(0, 1, 0)
>>> abs(v)
1.0

orthogonal(other)¶

Returns True if the two vectors are orthogonal to each other:

>>> a = Vector(3, 0, 0)
>>> b = Vector(0, 1, 1)
>>> a.orthogonal(b)
True

parallel(other)¶: Returns True if the two vectors are parallel to each other.

3.3. Lines¶

class sgl.line.Line(Point, Point)¶

class sgl.line.Line(Point, Vector)

class sgl.line.Line(Vector, Vector)

The Line class represents an infinitely long line in 3D space. You can specify a Line by two Points (1st form), in this case the resulting Line will be the one going through both Points.

Otherwise you can specify a Line by giving a single Point on the Line and a Vector showing the direction of the Line (2nd form). Instead of the Point itself you can also give the position vector of the Point (3rd form).

Operation	Result
`a in b`	Returns `True` if Point a lies on the Line b
`a == b`	Returns `True` if Lines a and b are the same, even though they might have different representations

parametric()¶: Returns a tuple of two vectors needed to describe the Line. Let (s, d) be the return value of the function, then the Line can be expressed as

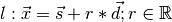
$l: \vec{x} = \vec{s} + r * \vec{d} ; r \in \mathbb{R}$

3.4. Planes¶

class sgl.plane.Plane(Point, Point, Point)¶

class sgl.plane.Plane(Point, Vector, Vector)

class sgl.plane.Plane(Point, Vector)

class sgl.plane.Plane(a, b, c, d)

The Plane class represents a plane in 3D space (not the flying plane).

In the 1st form a Plane is initialised by giving 3 points that are part of the plane.

In the 2nd form a Plane is initialised by giving an arbitrary point on the plane and two vectors lying on the Plane (they must not be parallel).

In the 3rd form a Plane is initialised by giving an arbitrary point on the plane and the normal vector of the plane, that is the vector that is orthogonal to the plane.

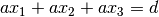
In the 4th form a Plane is initialised by giving the four coefficients of the general form $ax_{1} + ax_{2} + ax_{3} = d$

Operation	Result
`a in b`	Returns `True` if Point or Line a lies on the Plane b
`a == b`	Returns `True` if Planes a and b are the same, even though they might have different representations

general_form()¶: Returns (a, b, c, d), the coefficients for the general form

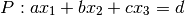
$P: ax_{1} + bx_{2} + cx_{3} = d$

parametric()¶: Returns vectors (s, u, v) for the parametric form

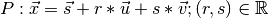
$P: \vec{x} = \vec{s} + r * \vec{u} + s * \vec{v} ; (r, s) \in \mathbb{R}$

point_normal()¶: Returns vectors (p, n) for the point-normal form

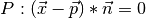
$P: (\vec{x} - \vec{p}) * \vec{n} = 0$

3.5. Calculating functions¶

The following functions work for any combination of Line and Plane.

sgl.calc.angle(a, b)¶: Returns the angle (in radians) between a and b.

sgl.calc.distance(a, b)¶: Returns the distance between a and b.

Note

This function also works with Point.

sgl.calc.intersection(a, b)¶

Returns the intersection of a and b. Depending on the Type of the intersection, this can return

None
A Point for Line/Line and Plane/Line intersections
A Line for Plane/Plane intersections

sgl.calc.orthogonal(a, b)¶: Returns True if a and b are orthogonal

sgl.calc.parallel(a, b)¶: Returns True if a and b are parallel

Note

If a is a Plane or a Line, a.distance(b) is the same as distance(a, b). The same goes for the angle, orthogonal, parallel and intersection functions.

3.6. Drawing¶

If you have vtk installed, you can use the draw() function to get a visual representation of your lines and planes.

sgl.draw.draw(elements[, background=(0.5, 0.5, 0.5), size=(640, 480), box=((-10, -10, -10), (10, 10, 10)), grid=(1, 0, 1)])¶

Open an interactive window with a visual representation of the given list of elements. Currently supported are

Vectors (pointing away from the origin)
Points (little spheres)
Lines
Planes

Parameters:

elements – The list of elements to draw
background – The (r, g, b) color of the background
size – The initial window size
grid – Defines if a coordinate grid should be drawn. It’s a tuple of three values for the (x1x2, x1x3, x2x3) planes. The value specifies the spacing between grid lines. If the value is 0, no grid for that plane will be drawn.
box – Defines the box in which planes/lines will be shown (as they are infinitely big)

See Examples for an example on how to use the draw function.

3. Class method reference¶

3.1. Points¶

3.2. Vectors¶

3.3. Lines¶

3.4. Planes¶

3.5. Calculating functions¶

3.6. Drawing¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

3. Class method reference¶

3.1. Points¶

3.2. Vectors¶

3.3. Lines¶

3.4. Planes¶

3.5. Calculating functions¶

3.6. Drawing¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation